About me

 

 

 

 

Our eyes , cameras and lenses - Part 2

Visual acuity and resolution

This is the second part of an article about the vision and how it is processed . If you have not seen the first part , I recommend you to read it before, clicking in this link: Our eyes , cameras and lenses - Part 1

Visual acuity

 

Imagine some horizontal lines that go thinning and approaching one another until we see them as to be one. This limit where we still see them separately determines the visual acuity of our eyes.

 

Studies have shown that in normal lighting conditions, human eye has the ability to distinguish pairs of lines separated by an angle of view up to a minute of a degree, that is, 1 /60°.

 

​

 

To understand how small is a minute of a degree angle, imagine a right angle (90°) like the corner of a room. Divide this angle by 90 and you will have the value of 1°, now divide it again by 60; this is our visual acuity.

 

For example, a speed dome with 35X optical zoom ranges from a 3.6 mm to 126 mm aperture. At maximum optical zoom, image you are seeing is with an opening angle of about 1.7º, still 102 times greater than our eyesight!

 

The Snellen Chart

 

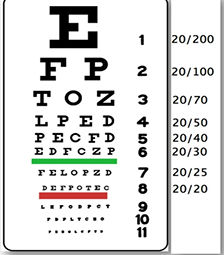In 1862, Dutch ophthalmologist Hermann Snellen, drafted the chart at left to test our visual acuity.

 

For this he considered the minimum angle of vision, a minute of a degree, already mentioned above.

 

Then he made letters of 20/20 line with 5 minutes high, being thickness and spacing of the letters 1 minute wide.

 

This letter was placed 20 feet away. Remember the ideal distance to our eyes, discussed in the first part?

 

At 20 feet away, our ciliary muscles are relaxed, the best condition to test our visual acuity.

 

According to Snellen calculations, if  20/20 line of letters have a 8.75 mm height, a person with normal vision can perfectly read this line at 20 feet away.

 

This information is important to know how to better observe images captured by cameras in accordance with its resolution, display's resolution, screen size and best distance from operator.

 

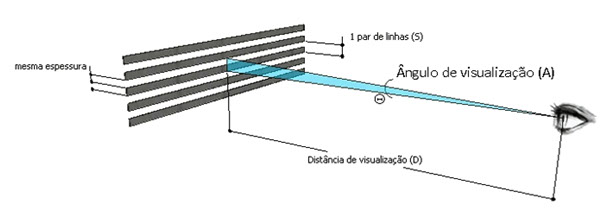
From that we will find what would be minimum size (S) pair of lines at the first figure of this article can has.

 

Using the formula S = tan (A) x D we will have that minimum size of that pair of lines is equal to the tangent of 1 /60° multiplied by distance. The tangent of 1 /60° is equal to 0.000291, that we can round up to 3/10000.

 

This makes it easy to find the minimum acceptable size of a pair of pixels (2 lines) on a monitor: Just multiply the distance (in feet) to the operator by 3 and divide it by 10,000.

 

For example, for an operator at 13 feet away from the monitor, a pair of pixels can be 0.047".

 

If monitor measures 25.6" vertical (52"), we will have 1083 pixels vertically (25.6/0,0235).

 

Then a monitor with these dimensions, having a 1080p resolution, at full-screen exhibiting the image of camera with this same resolution, will be in the ideal setting to be observed at this distance.

 

At a greater distance, we will lose the definition between these two lines. If operator becomes closer than that, begin to see the pixels of the image.

 

Our vision is curved

 

Visual acuity is specified as an angular measure (1/60°) not linear - like x inches - because our cornea is curved.

 

This means that we see in the same focal distance objects arranged in a curvature compatible with the curvature of the cornea.

 

So when we visualize distant things which are arranged in the same plane, we see the ends out of focus from the central region.

 

So every time we move our eyes to see the ends, our ciliary muscles will have to readjust the focus of our crystalline, contributing to a greater eye strain.

 

See how industry is been applying this knowledge:

 

- Up to the seventies, car panels were flat, with all instruments aligned in the same plane, pointing forward not to driver's position. Today panels are curved, engaging with all instruments on the same line of view to the driver;

 

- The latest craze are 4K TVs with curved screens...

 

Movie theaters and billboards

 

Movie Theaters

 

We can learn a lot from movie theaters. See how designers knew well to take advantage of the characteristics of our vision:

 

- All seats are over 6 feet away from the screen, enabling our ciliary muscles to be relaxed. So do we;

 

TIP As it isn't possible to design a room that is ideal for everyone, design takes into account the center of the room. So next time you go to the movies, try to sit in the center of the middle row, which is the best position to enjoy the movie. It's also the best position to enloy movie's sound effects- Screen size and high resolution projection allow an exact identification of objects and people in the film , even for those seated in the back ;

 

- Viewing angle is within the area covered by our cones (except for those who sit too close to the screen ... ), allowing better image definition and color identification; without that we would need to keep moving our eyes constantly;

 

- The dark room brings the focus of our vision to the screen , prioritizing our color and high definition vision (cones).

 

On the other hand, as time passes by, you start seeing better people who are in the room. That's because our rods are being adapted to the dark.

 

Billboards

 

If you have had the curiosity to look a billboard closely, you realized that image is not continuous, consisting of spheres of about 1" diameter each!

 

However, at the distance in which they are displayed , these spheres merge, forming an image with photographic quality.

 

This proves that definition has to do with screen size and viewing distance.

 

Human eye's resolution

 

Note that we are always talking about vertical resolution, because our eyes are more sensitive to vertical resolution than the horizontal.

 

It is for this reason that a Full HD image, which has 1920 x 1080 pixels, is called 1080p and not as 1920p, since what matters is the vertical resolution.

 

But what would be the equivalent resolution of the human eye in Megapixels?

 

At a distance of 25 cm, usually used for reading 1' (one minute degree) corresponds to about 350 ppi (pixels per inch).

 

When Apple released the new displays for the iPhone and iPad with 326 ppi resolution, close to the resolution of our retina, they were called Retina Displays. Now we have smart phones with more than 440 ppi.

 

If you search on Google which is the human eye resolution, you will find several websites saying it is 576 megapixels for an angle of 120°.

 

But what most impacts our perception is our central vision, where cones are concentrated (color and definition, remember?), which is about 20 ° from the center of the eye, 40° in total.

 

Just out of the edge of this range, a little more than 20°, resolution is already 10 times smaller!

 

It is easy to prove this: Look at the center of a line of pictures hung on a wall or objects on a shelf, colorful preferably, from about a meter away.

 

Still looking forward, try to see at the eye corner the picture or object to the left or right and you will notice how it is very blurry.

 

That is, the area of ​​our vision that matters when we are looking at cameras that are being viewed on a monitor, are only 40° front.

 

If these monitors are outside of this viewing angle, operators will have to be constantly moving their heads, which can be quite uncomfortable.

 

That's why I found very creative and correct the method used in this site to compare our view with Megapixel cameras:

 

http://ipvm.com/report/testing_the_resolution_of_the_human_eye

 

Positioning a Snellen chart at 20 feet away, they compared resolutions of multiple cameras (720p , 1080p , 5 MP and 10 MP) with human eye's to know up which line of Snellen chart they would be able to identify.

 

All lenses were with an aperture of 60°, close to human eye's angle of view, and tests were made ​​with different levels of lighting : 160 Lux , 3 Lux and 1 Lux.

 

Maximum resolution that each camera has been reached was:

 

​160 Lux20/2020/5020/4020/3020/201 Lux20/4020/10020/70BlindBlind3 Lux20/3020/7020/7020/5020/40 Human eye720p camera1080p camera5 Megapixels camera10 Megapixels camera

 

Test shows that in good lighting conditions, resolution of the human eye is equivalent to that of a 10 Megapixel camera.

 

However, for lower levels of light, human eye was far better than any of tested cameras.

 

Only flaw I found in this test is that, precisely in the area where it could detect resolution with better precision, there is a big jump setting from 5 to 10 Megapixels. Thus, it shows that 5 Megapixels is below human eye resolution, but any resolution between 5 and 10 Megapixels may be the point where a camera begins to match the human eye.

 

4 K, the Ultra HD, is it the limit? Based on the 2200 vertical pixels in our view, one can say that. Any resolution above 4K would be useless, because it would be setting up our eyes. Well, for entertainment, maybe. This is a discussion that's been worrying TV makers. But for CCTV applications, the higher the resolution, the higher the digital zoom capability, allowing you to capture more image details.For this reason, we must consider the information obtained in other studies, which proved to be resolution to the human eye equivalent of 8 Megapixels .

 

At minimum angle permitted by our visual acuity (1/60°) and given the dimensions of the cornea, it was determined that vertical resolution of our eyes is about 1100 pairs of rows, that is , equivalent to 2200 pixels.

 

An 8 megapixel camera for 4K resolution is about 3840 x 2160 pixels, near to the 2200 vertical pixels of our eyes, which proves the result obtained above.

 

The ideal monitoring room

 

Based on what we learn, an ideal monitoring room should consider the following:

 

- For ciliary muscles work relaxed, operator should be at a minimum distance of 20 ft from the monitors ;

 

- Each operator should be responsible only for displays that are within a viewing angle at 40 ° maximum ;

 

- Monitors should preferably be installed in a curve, both vertically and horizontally, so that everyone is on the same focal length for the operator and the ideal location for this operator is looking at the center of this array of monitors.

 

- The rods, which capture more light, are mostly in our peripheral vision. Therefore, the lighting of the room should be reduced to not disrupt the viewing of the monitors, which will be made more through the cones within the 40° opening;

 

- All monitors must be the same distance from the operator.

 

MAKE THIS TEST With room lights off, but not totally dark, look to the side so that your monitor is in your peripheral vision. You will notice two things: - Monitor screen will become blurred, as is now being viewed by the rods, which have a resolution more than ten times lower than that of cones; - You can not properly define objects that are next to the monitor, due to screen brightness being in your peripheral vision. Turn monitor off. Now you can better define objects near monitor.Try to avoid, when possible, near monitors, which have a much higher brightness and would complicate to visualize the distant ones.

 

As when operator is viewing far monitors, individual monitor shall be in his peripheral vision, with its light being amplified by his rods.

 

In addition, for the reasons already explained , the constant shift near-far would cause greater visual fatigue.

 

I know that this item is difficult to meet , because usually each operator has an individual computer and monitor.

 

If that can not be avoided, try to adjust individual monitor brightness to an intensity compatible with distant monitors, try to put it aside or below or even turn it off when not in use.

 

Applying the above assumptions to the following example, in scale, we have a room where operator is 20 ft away from monitors, his 40° viewing angle covers an area of 13.5 ft horizontally, where is installed 4 x 47 "monitors ( 47"/1.15 = 40.86") following the bend angle .

 

​

 

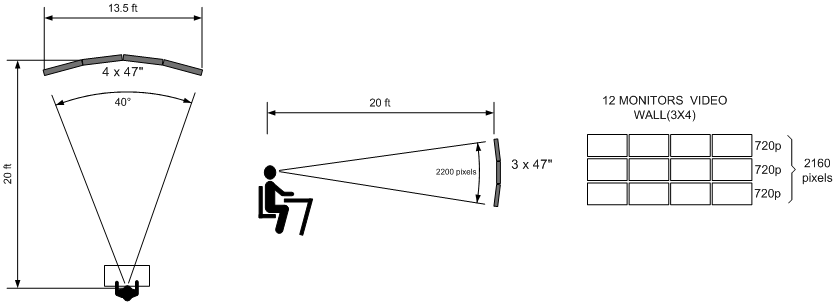
At the vertical, our vision covers 2200 pixels. Then 3 monitors with 720p resolution will add 2160 pixels , given the desired resolution.

 

Thus, the operator is able to view a video wall with 12 monitors of 47 " with 720p resolution each.

 

Probably each monitor will be most of the time with its screen splitted, displaying multiple cameras. These calculations are made for a camera being visualized in full-screen which is when you want more details of the image, when you need the best possible display resolution .This solution would display 12 HD (720p) cameras.

 

However, if cameras are Full HD (1080p ), we have to use 1080p displays, but piling 2 of them already attend the desired resolution.

 

Therefore, operator would see only 8 (4x2) monitors at Full HD.

 

That would be the ideal condition, more ergonomic, as it allows operator to see all monitors in their best resolution without the need of moving his head nor readjusting the focus of his vision.

 

What if room is not ideal?

 

It's not always that we will get a room where we can sit an operator 20 feet away from a wall. Therefore, we will have to adapt the ideal conditions for the maximum available distance. Remember that the eyes of the operator won't be relaxed in this setting.

 

To make this adjustment:

 

1- Multiply the distance operator will be from the monitors by 0.64. This is the width of the area covered by operator's vision;

 

2 - Divide the size of the desired monitor for 1.15 to get its width. Check how many monitors will be needed to cover the width obtained in item 1. If it does not fit an exact number or near, increase or decrease the size of the monitors;

 

3 - Specify the definition of monitors as the definition of cameras that are displayed;

 

4 - Check how many monitors will be stacked vertically to achieve 2200 pixels.

 

This is the maximum number of cameras / monitors that each operator be able to view comfortably.

 

If you don't need so many monitors, do the calculation for maximum monitors and use only the amount you need, grouping them in the center.

 

This is necessary to ensure that monitors will be at the most appropriate distance / resolution.

 

Conclusion

 

Nature is wise, simple, efficient and straightforward.

 

And we ever get right when we design something based on what nature has been using for thousands - or millions - of years.

 

One example is  that scientists been  struggling for a long time to design more efficient solar cells.

 

Recently, someone decided to copy our eyes, transforming solar cells structures in cones, this had  increased light absorption by 65% ​​...

 

​

 

 

Mar/2015

Dec/2015

TIP

 

Nowadays monitors usually have a 16:9 ratio between width and height and its dimensions are specified by its diagonal, in inches.

 

So to know the approximate height of a monitor, divide its diagonal by 2.04. To know the width, divide it by 1.15.

Inserir nome

Just iinform your e-mail to be aware of every update in this website. Put your e-mail here

Enviando formulário…

O servidor encontrou um erro.

Formulário recebido.